I. 합병 정렬 (Merge Sort)의 개요
가. 합병 정렬의 정의
- 리스트를 두 개로 나누어, 각각을 정렬한 다음, 다시 하나로 합치는 정렬 방법
나. 합병 정렬의 특징
- 분할과 정복 : 분할(Divide) -> 정복(Conquer) -> 결합(Combine) 과정 수행
- 재귀적 수행 : 분할을 마친 후 분할된 부분의 반복적 수행
- 정렬을 위한 별도의 공간이 필요
- 수행시간 복잡도: O(n·log2n)
Ⅱ. 합병 정렬의 단계 및 사례
가. 합병 정렬의 단계
 |
나. 합병 정렬 개념
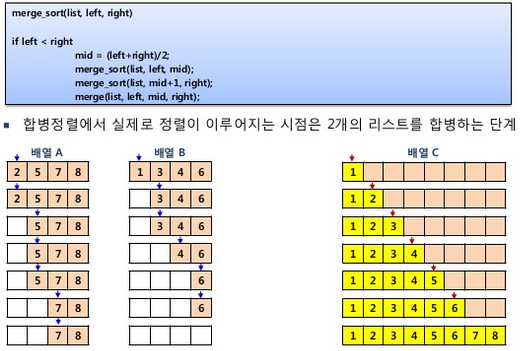 |
| void mergeSort(int arr[], int l, int r) { if (l < r) { int m = l+(r-l)/2; //Same as (l+r)/2, but avoids overflow for large l and h mergeSort(arr, l, m); mergeSort(arr, m+1, r); merge(arr, l, m, r); } } void merge(int arr[], int l, int m, int r) { int i, j, k; int n1 = m - l + 1; int n2 = r - m; /* create temp arrays */ int L[n1], R[n2]; /* Copy data to temp arrays L[] and R[] */ for(i = 0; i < n1; i++) L[i] = arr[l + i]; for(j = 0; j < n2; j++) R[j] = arr[m + 1+ j]; /* Merge the temp arrays back into arr[l..r]*/ i = 0; j = 0; k = l; while (i < n1 && j < n2) { if (L[i] <= R[j]) { arr[k] = L[i]; i++; } else { arr[k] = R[j]; j++; } k++; } /* Copy the remaining elements of L[], if there are any */ while (i < n1) { arr[k] = L[i]; i++; k++; } /* Copy the remaining elements of R[], if there are any */ while (j < n2) { arr[k] = R[j]; j++; k++; } } |
'IT 용어 및 개념 > Algorithm' 카테고리의 다른 글
| [Algorithm] 버블 정렬 (Bubble Sort) (0) | 2024.09.14 |
|---|---|
| [Algorithm] 해시 탐색 (Hash Search) (0) | 2024.09.14 |
| [Algorithm] 이진 탐색 (Binary Search) (0) | 2024.09.14 |
| [Algorithm] 삽입 정렬 (Insert Sort) (0) | 2024.09.14 |
| [Algorithm] 순차 탐색 (Sequential Search) (0) | 2024.09.14 |
