[Algorithm] 최단 경로 탐색 알고리즘

I. 최단 경로 탐색의 개요

가. 최단 경로 탐색의 정의

그래프 내의 한 vertex에서 다른 vertex로 이동할 때 가중치의 합이 최솟값이 되는 경로를 탐색하는 알고리즘

최단 경로 탐색의 정의

 

Ⅱ. 최단 경로 탐색 알고리즘

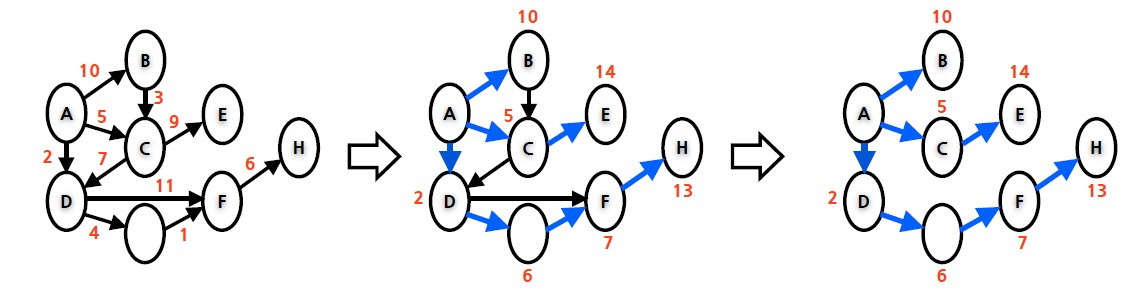
가. 다익스트라 알고리즘 (Dijkstra Algorithm)

* 사이클이 없는 방향성에만 적용 * 가중치 합 최소 * Link State 알고리즘 활용 각 vertex들은 시작점으로부터 자신에게 이르는 경로의 길이를 저장할 곳을 준비 모든 vertex들은 경로의 길이를 무한대로 초기화 시작 vertex의 경로의 길이를 0으로 초기화하고 최단 경로에 추가 연결된 vertex들의 경로 길이를 갱신 인접한 vertex가 최단 경로에 이미 존재하면, 이전 경로 길이와 비교, 작으면 수정, 크면 무시 그래프 내의 모든 vertex들이 최단 경로로 만들어질 때까지 4~5 반복

function Dijkstra(Graph, source): dist[source] := 0 // Distance from source to source for each vertex v in Graph: // Initializations if v ≠ source dist[v] := infinity // Unknown distance function from source to v previous[v] := undefined // Previous node in optimal path from source end if add v to Q // All nodes initially in Q end for while Q is not empty: // The main loop u := vertex in Q with min dist[u] // Source node in first case remove u from Q for each neighbor v of u: // where v has not yet been removed from Q. alt := dist[u] + length(u, v) if alt < dist[v]: // A shorter path to v has been found dist[v] := alt previous[v] := u end if end for end while return dist[], previous[] end function

 

나. 벨만-포드 알고리즘(Bellman-Ford Algorithm)

* 사이클이 없는 방향성에만 적용 * 가중치의 음수 값도 고려 * Distance Vector 알고리즘 활용 각 vertex들은 시작점으로부터 자신에게 이르는 경로의 길이를 저장할 곳을 준비 모든 vertex들은 경로의 길이를 무한대로 초기화 시작 vertex의 경로의 길이를 0으로 초기화하고 최단 경로에 추가 음의 가중치를 고려하면서 연결된 vertex들의 경로의 길이를 갱신 인접한 vertex가 최단 경로에 이미 존재하면, 이전 경로의 길이와 비교, 작으면 수정, 크면 무시 그래프 내의 모든 vertex들이 최단 경로로 만들어질 때까지 4~5 반복

function BellmanFord(list vertices, list edges, vertex source) ::distance[],predecessor[] // Step 1: initialize graph for each vertex v in vertices: distance[v] := inf // At the beginning , all vertices have a weight of infinity predecessor[v] := null // And a null predecessor distance[source] := 0 // Except for the Source, where the Weight is zero // Step 2: relax edges repeatedly for i from 1 to size(vertices)-1: for each edge (u, v) with weight w in edges: if distance[u] + w < distance[v]: distance[v] := distance[u] + w predecessor[v] := u // Step 3: check for negative-weight cycles for each edge (u, v) with weight w in edges: if distance[u] + w < distance[v]: error "Graph contains a negative-weight cycle" return distance[], predecessor[]

 

다. 플로이드 알고리즘

* 그래프에 존재하는 모든 정점 사이의 최단 경로를 한 번에 찾아주는 알고리즘 * 2차원 배열을 사용하여 3중 반복을 하는 루프로 구성 * 인접행렬 weight 구성 시작 지점을 i==j이면, weight[i][j]=0 두개의 정점 i,j 사이에 간선이 존재하지 않으면, weight[i][j]=∞ 정점 i,j 사이에 간선이 존재하면, weight[i][j]는 간선 (i, j)의 가중치 배열 A의 초기 값은 인접 행렬 weight임

shortest_floyd(int adj_matrix[][]){ dist[SIZE][SIZE]; dist[][] = adj_matrix[][]로 초기화 for(k=0; k < n; k++) for(i = 0; i < n; i++) for(j =0; j < n; j++) dist[i][j] = Min(dist[i][j], dist[i][k] + dist[k][j]); return(dist); }

 

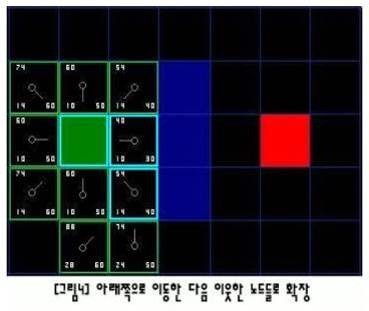
라. A* 알고리즘 (A* Algorithm)

* 시작지점에서 목표지점까지의 경로탐색을 위하여 휴리스틱 함수를 사용 시작 지점을 열린 목록에 넣는다. 열린 목록에 있는 노드 중 1개를 빼서 여덟 방향 주변 노드를 탐색한다. 2단계에서 뺀 노드를 닫힌 목록에 삽입한다. 2단계에서 탐색한 노드들을 열린 목록에 삽입한다. 열린 목록 중에서 가장 앞 노드를 빼고 그 노드를 닫힌 목록에 추가한다. 5단계에서 뺀 노드의 여덟 방향 주요 노드를 탐색한다. 열린 목록에 존재하지 않는 노드는 열린 목록에 추가하고 중복되는 노드는 G값을 서로 비교하며 더 작은 값을 열린 목록으로 교체한다. 5단계부터 반복
초록색은 시작위치, 빨강색은 목표위치, 파란색은 장애물로서 지나갈 수 없는 위치