[Algorithm] 힙 정렬 (Heap Sort)

I. 힙 정렬 (Heap Sort)의 개요

가. 힙 정렬의 정의

트리 중에서 부모 노드의 원소 값이 자식 노드의 원소 값보다 큰 완전 이진 트리인 힙(Heap)을 만들기 위한 정렬 방법

나. 힙 정렬의 특징

• 힙 구조에서 가장 큰 값의 위치는 루트에 있음.
• 배열에 저장하는 것이 효율적임.
• 수행시간 복잡도: O(n·log2n)

 

Ⅱ. 힙 정렬의 삽입∙삭제 과정 및 사례

가. 힙 정렬의 삽입과정 및 사례

새로운 노드의 위치를 정한다. 삽입할 데이터를 새로운 노드에 놓는다. 새로운 노드와 부모를 비교하여 부모가 더 작으면 바꾸는 과정을 루트에 도달할 때까지 계속한다.
	⇒		⇒		⇒
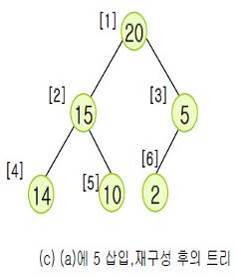void insert_max_heap(element item, int *n) { int i; if(HEAP_FULL(*n)) { fprintf(stderr,”The heap is full. ₩n”); exit(1); } i = ++(*n); while((i!=1)&&(item.key>heap[i/2].key)) { heap[i] = heap[i/2]; i /= 2; } heap[i] = item; }

 

나. 힙 정렬의 삭제과정 및 사례

마지막 레벨의 마지막 노드를 루트에 올려 놓는다. 루트노드를 왼쪽 혹은 오른쪽 자식노드(왼쪽과 오른쪽 중 큰 값)와 교환한다. 2번 과정을 트리의 밑으로 내려가면서 계속 반복한다.
	⇒		⇒		⇒
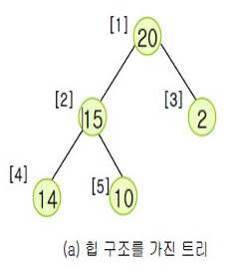element delete_max_heap(int *n) { element item, temp; if(HEAP_EMPTY(*n)) { fprintf(stderr,”The heap is empty₩n”); exit(1); } item = heap[1]; temp = heap[(*n)--]; parent = 1; child = 2; while(child <= *n) { if((child < *n) && (heap[child].key < heap[child+1].key)) child++; if(temp.key>=heap[child].key) break; heap[parent] = heap[child]; parent = child; child *= 2; } heap[parent] = temp; return item; }